Motivation Integralrechnung

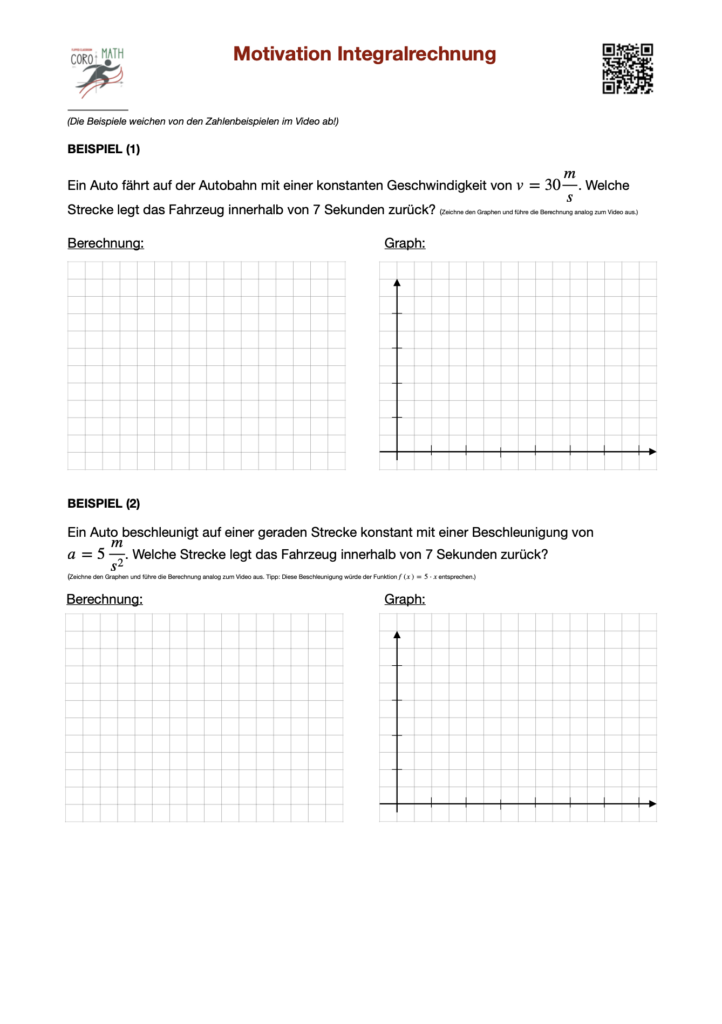
Die Integralrechnung und die Differentialrechnung sind eng miteinander verknüpfte Gebiete der Mathematik. Während die Differentialrechnung sich mit der Änderung von Funktionen beschäftigt – also zum Beispiel, wie schnell sich etwas verändert –, befasst sich die Integralrechnung mit der Frage, wie viel sich im Laufe der Zeit oder in einem bestimmten Bereich ansammelt. Man könnte sagen, dass die Differentialrechnung den Blick auf die Details richtet, während die Integralrechnung das Gesamtbild betrachtet.

Ein klassisches Beispiel für den Zusammenhang zwischen den beiden Gebieten ist das Thema Geschwindigkeit und Strecke: Die Differentialrechnung beschreibt die Geschwindigkeit eines Objekts zu einem bestimmten Zeitpunkt, also wie schnell es sich bewegt. Die Integralrechnung summiert diese kleinen Änderungen der Geschwindigkeit auf und gibt uns die insgesamt zurückgelegte Strecke.

Mathematisch gesehen ist das Integral das Gegenteil (oder das „Umkehrverfahren“) der Ableitung. In der Praxis bedeutet das: Wenn man die Ableitung einer Funktion kennt, kann man durch Integration die ursprüngliche Funktion wiederherstellen. Dieser Zusammenhang, bekannt als der Hauptsatz der Differential- und Integralrechnung, zeigt, wie diese beiden Rechenmethoden zusammenarbeiten, um komplexe Probleme der Mathematik zu lösen – von der Berechnung von Flächen bis hin zur Analyse von Bewegungen und Wachstumsprozessen.

Viel Spaß bei diesem Kurs! 🙂