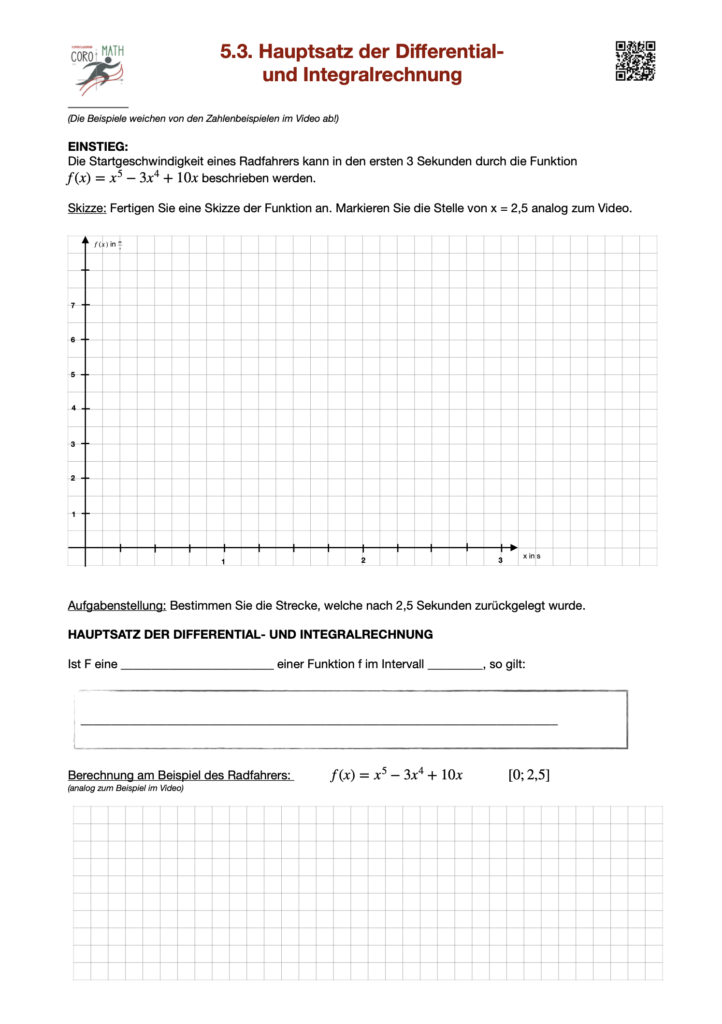
Hauptsatz der Differential- und Integralrechnung

Der Hauptsatz der Differential- und Integralrechnung ist ein mächtiges Werkzeug in der Mathematik, das zahlreiche Anwendungen in der Physik, Ingenieurwissenschaft und vielen weiteren Disziplinen ermöglicht. Sein zentraler Nutzen liegt in der Verknüpfung von Differentiation und Integration, zwei grundlegenden Konzepten der Analysis. Dies eröffnet einen effizienten Weg, komplizierte Berechnungen zu vereinfachen und Integrale schnell zu lösen.

Durch den Hauptsatz lässt sich das Berechnen bestimmter Integrale auf das Auffinden einer Stammfunktion reduzieren, was die Arbeit erheblich erleichtert. So können Flächeninhalte, Volumina oder physikalische Größen wie Geschwindigkeit und Strecke problemlos ermittelt werden. Insbesondere bei physikalischen Modellen, in denen Bewegungen, Kräfte oder Energieverläufe analysiert werden, erlaubt der Hauptsatz eine schnelle Berechnung von Gesamteffekten durch Integration.

Darüber hinaus hilft der Hauptsatz, mathematische Zusammenhänge besser zu verstehen, indem er den Übergang zwischen lokalen (Ableitungen) und globalen (Integrale) Eigenschaften einer Funktion deutlich macht. Dies ist nicht nur in der Theorie von Bedeutung, sondern auch in der Praxis, wo komplexe dynamische Systeme oft durch die Verknüpfung dieser Konzepte beschrieben werden. Der Hauptsatz ist somit ein unverzichtbares Instrument in der angewandten Mathematik und den Naturwissenschaften.

Viel Spaß bei diesem Kurs! 🙂