Berechnung von Flächeninhalten
Oder: Warum man ab jetzt wirklich jede Fläche berechnen kann.
Die Kapitel
Was erwartet dich
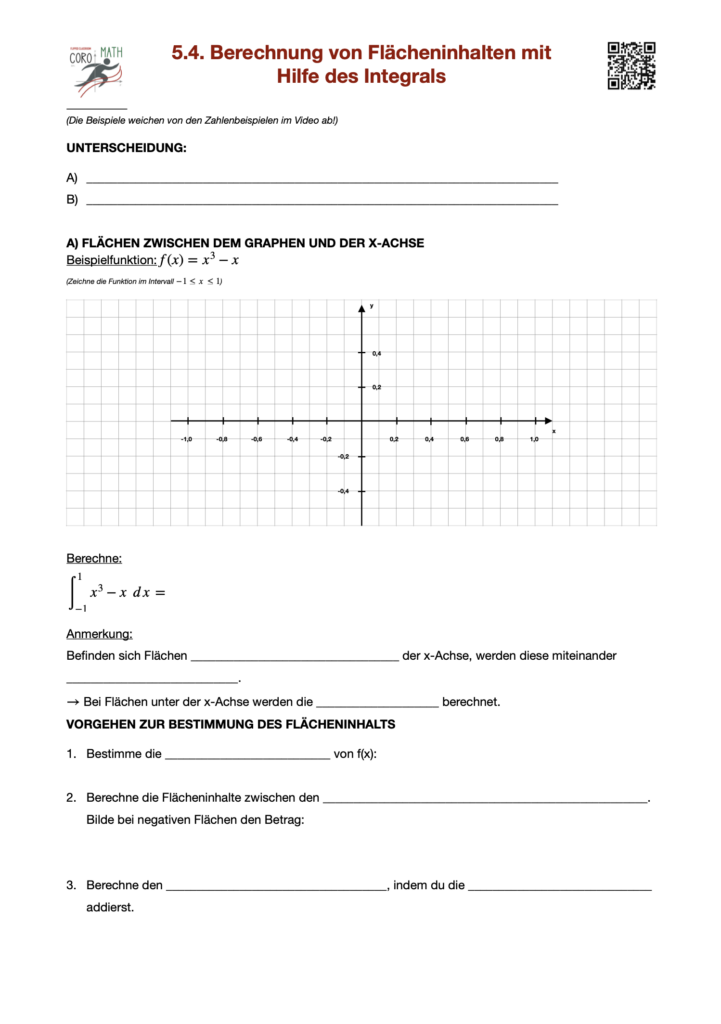
Die Flächenberechnung mithilfe des Integrals ist eine der wichtigsten Anwendungen der Integralrechnung in der Mathematik. Durch das bestimmte Integral lässt sich die Fläche unter einer Kurve, die von einer Funktion f(x)f(x)f(x) über einem Intervall [a,b][a, b][a,b] beschrieben wird, exakt bestimmen. Dabei gibt das Integral die Summe unendlich vieler unendlich kleiner Flächenstücke an, die unter der Kurve liegen.
Mathematisch wird diese Fläche durch das bestimmte Integral \int_a^b f(x)dx dargestellt. Hierbei sind aaa und bbb die Grenzen des Intervalls, über das die Fläche berechnet wird. Die Funktion f(x)f(x)f(x) beschreibt den Verlauf der Kurve, und das Integral liefert die exakte Fläche zwischen der Kurve und der x-Achse.
Ist die Kurve oberhalb der x-Achse, entspricht der Wert des Integrals der gesuchten Fläche. Liegt die Kurve teilweise unterhalb der x-Achse, muss der Betrag des Integrals betrachtet werden, da das Integral in diesem Fall negative Flächenanteile liefert.
Diese Methode zur Flächenberechnung hat zahlreiche Anwendungen in der Physik, Ingenieurwissenschaft und Ökonomie, da sie eine präzise Berechnung von Flächen unter Funktionen ermöglicht, die durch andere Verfahren schwer zugänglich wären.
Viel Spaß bei diesem Kurs! 🙂
Materialien
Arbeiten mit den Materialien
Um mit den Materialien arbeiten zu können, gehst du wie folgt vor:
- Klicke auf das Bild rechts neben dem Text
- Lade dir die PDF herunter und drucke das Blatt aus (Tipp: Am besten Doppelseitig)
- Sehe dir das unten verlinkte Lernvideo an.
- Fülle die Lücken auf dem Blatt parallel zum Video aus.
- Übe mit den Übungsaufgaben.
- Überprüfe ob du das Blatt richtig ausgefüllt. Klicke dafür auf das Bild im Fenster Kontrolle.
Lernvideo
Übungsaufgaben
Aufgabe Versuche dich an den folgenden interaktiven Aufgaben! (folgt noch)