Tangente und Normale an Funktionen
Die Kapitel
Was erwartet dich
Wenn wir den Graphen einer ganzrationalen Funktion betrachten, also einer Funktion, die durch ein Polynom beschrieben wird, interessiert uns oft, wie wir die Lage einer Tangente oder einer Normalen an einem bestimmten Punkt bestimmen können. Die Tangente ist eine gerade Linie, die den Graphen an genau einem Punkt berührt und die Richtung des Graphen an dieser Stelle widerspiegelt. Sie ist wie eine Momentaufnahme der Funktion, die uns zeigt, wie steil der Graph in diesem Punkt verläuft. Die Normale ist eine Linie, die senkrecht zur Tangente steht und damit den Graphen im gleichen Punkt schneidet.
Um eine Tangente oder eine Normale zu berechnen, benötigen wir den Punkt auf dem Graphen, an dem wir die Berührungspunkte bestimmen wollen, sowie die Ableitung der Funktion an dieser Stelle. Die Ableitung gibt uns die Steigung der Tangente, während die Normale eine Steigung hat, die der Kehrwert und das Vorzeichen der Tangentensteigung ist.
Diese Berechnungen sind nicht nur in der Mathematik, sondern auch in der Physik und Technik von großer Bedeutung, etwa bei der Analyse von Bewegungen, der Optimierung von Prozessen oder der Untersuchung von Kurvenverläufen in der Praxis. Die Fähigkeit, Tangenten und Normalen zu berechnen, ermöglicht es uns, das Verhalten von Funktionen noch besser zu verstehen und zu modellieren.
Viel Spaß bei diesem Kurs! 🙂
Materialien
Arbeiten mit den Materialien
Um mit den Materialien arbeiten zu können, gehst du wie folgt vor:
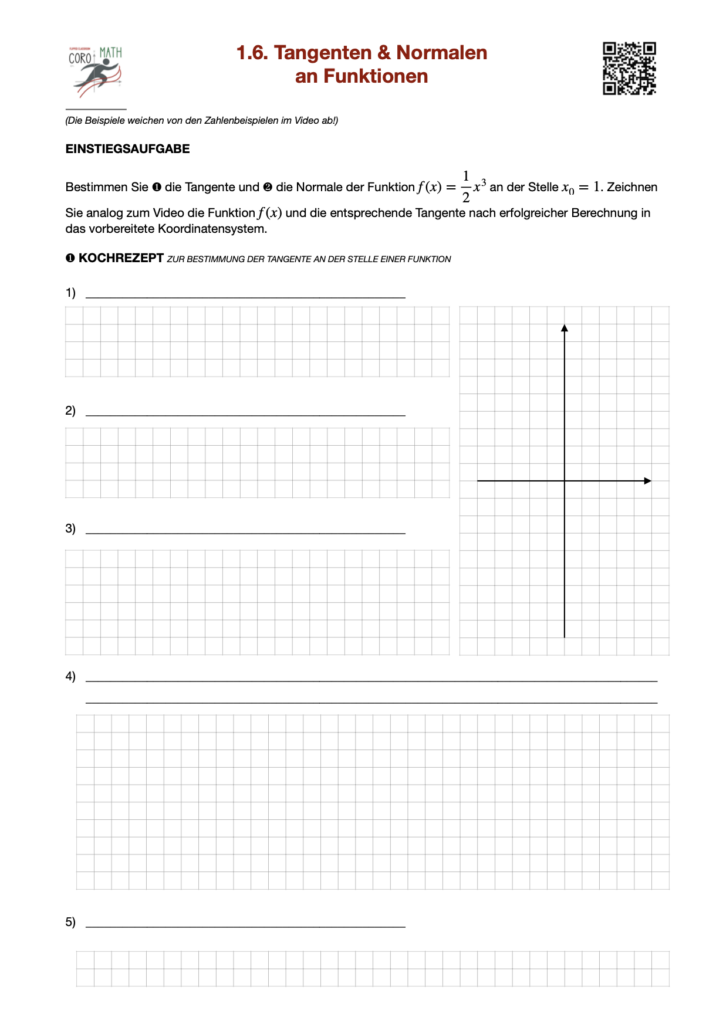
- Klicke auf das Bild rechts neben dem Text
- Lade dir die PDF herunter und drucke das Blatt aus (Tipp: Am besten Doppelseitig)
- Sehe dir das unten verlinkte Lernvideo an.
- Fülle die Lücken auf dem Blatt parallel zum Video aus.
- Übe mit den Übungsaufgaben.
- Überprüfe ob du das Blatt richtig ausgefüllt. Klicke dafür auf das Bild im Fenster Kontrolle.
Lernvideo
Übungsaufgaben
Aufgabe Versuche dich an den folgenden interaktiven Aufgaben!
Tangentenberechnung an Funktionen
Aufgabe 2 Bestimme den gesuchten Anstieg und überprüfe dein Ergebnis grafisch mit Hilfe der unten verlinkten Animation.
Tangente zeichnen
Lernst du gern mit Coromath?
Dann hilf uns und abonniere den YouTube-Kanal "Coromath"
Aktuell produziert die WebSite noch geringe Kosten. Mit der Implementierung weiterer Funktionen steigen diese. So wäre die Einbindung einer KI zum beantworten von Fragen möglich, jedoch auch sehr teuer. Daher freuen wir uns über jede Unterstützung, welche uns die Seite ausbauen lässt. Eine Einnahmemöglichkeit wäre die Monetarisierung des dazugehörigen YouTube-Kanals. Für ein Abo musst du nur auf das nebenstehende Bild klicken.