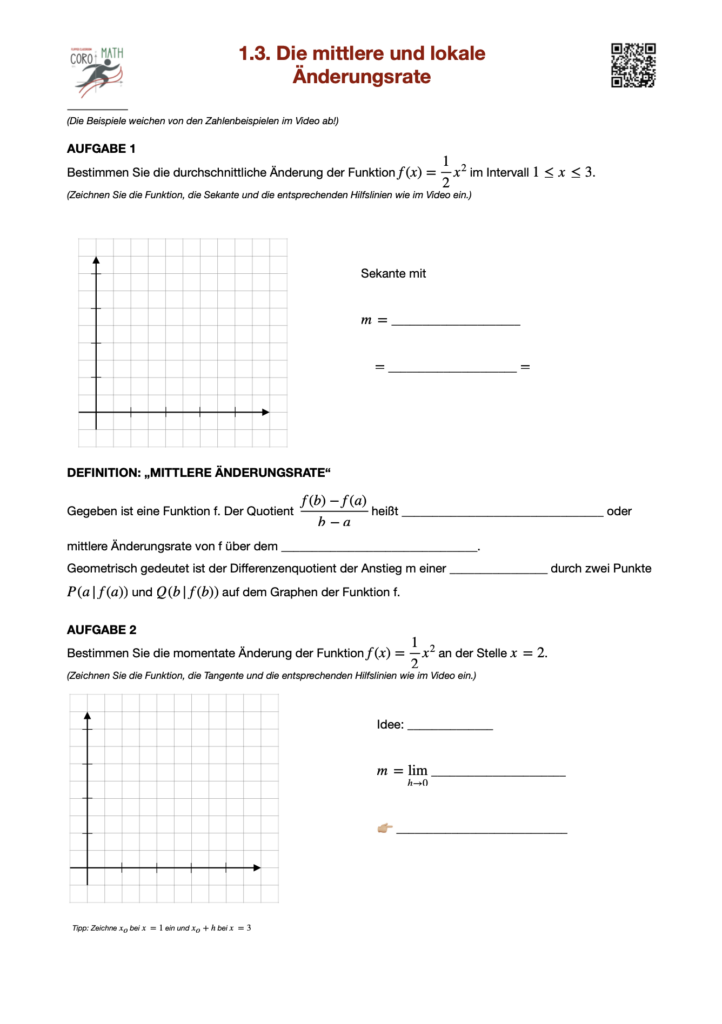
Die mittlere und lokale Änderungsrate

Wenn wir uns in der Mathematik mit Funktionen beschäftigen, interessiert uns oft nicht nur, welche Werte die Funktion annimmt, sondern auch, wie sich diese Werte verändern, wenn wir die Eingabewerte der Funktion ändern. Dieses Interesse führt uns zu einem zentralen Konzept: der Änderungsrate. Die Änderungsrate gibt uns eine Vorstellung davon, wie schnell oder langsam die Funktion steigt oder fällt, wenn wir uns entlang ihres Graphen bewegen.

Ein einfaches Beispiel aus dem Alltag kann helfen, dieses Konzept zu verstehen. Stell dir vor, du fährst mit dem Fahrrad einen Hügel hinauf. Der Hügel repräsentiert den Graphen einer Funktion, wobei die Höhe die Ausgabewerte und die Entfernung die Eingabewerte darstellt. Manchmal steigt der Hügel steil an, manchmal flach. Die Steilheit, die du spürst, entspricht der Änderungsrate der Funktion an verschiedenen Punkten.

Zwei Begriffe sind hier besonders wichtig: die mittlere Änderungsrate und die lokale Änderungsrate. Während die mittlere Änderungsrate eine Art Durchschnitt der Steilheit zwischen zwei Punkten auf dem Hügel beschreibt, gibt die lokale Änderungsrate Auskunft über die Steilheit an einem ganz bestimmten Punkt.

Doch warum ist es überhaupt wichtig, diese Raten zu betrachten? Was verraten sie uns über die Funktion und ihre Eigenschaften? Die Antworten auf diese Fragen führen uns tiefer in das Verständnis der Funktionsanalyse und sind entscheidend für viele Anwendungen in Wissenschaft, Technik und Wirtschaft.