Die Bogenlänge einer Funktion
Oder: Wie weit man eine Funktion ablaufen muss.
Die Kapitel
Was erwartet dich
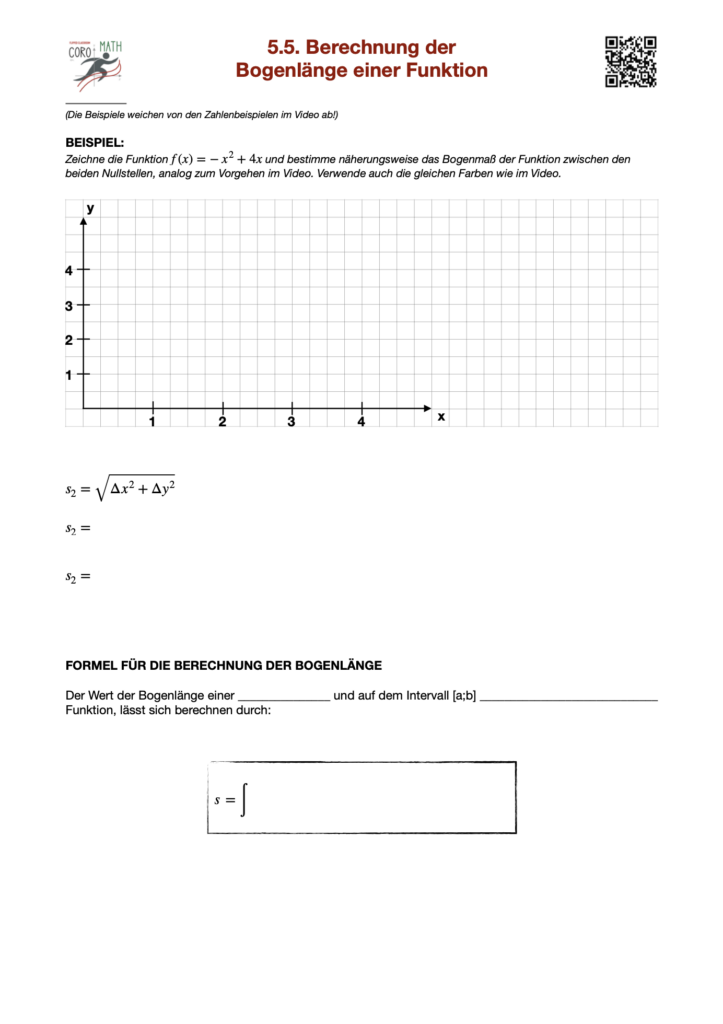
Die Bestimmung der Bogenlänge einer Funktion ist ein grundlegendes Konzept in der Analysis, das es ermöglicht, die genaue Länge einer Kurve im zweidimensionalen Raum zu berechnen. Anders als bei geraden Linien, deren Länge einfach durch die Differenz der Endpunkte ermittelt werden kann, erfordert die Berechnung der Bogenlänge von gekrümmten Funktionen ein tieferes mathematisches Verständnis.
Die Bogenlänge ist besonders wichtig in zahlreichen Anwendungsbereichen wie der Physik, Ingenieurwissenschaft und Geometrie. Beispielsweise spielt sie eine entscheidende Rolle bei der Berechnung von Strecken in der Bewegungskinematik, bei der Gestaltung von Straßen und Bahnwegen oder bei der Analyse von Wellenformen in der Elektrotechnik. Durch die Bestimmung der Bogenlänge können präzise Modelle erstellt werden, die komplexe Phänomene realitätsnah abbilden.
Um die Bogenlänge einer Funktion zu berechnen, wird die Funktion zunächst differenziert, um ihre Steigung an jedem Punkt zu bestimmen. Anschließend werden diese Steigungen integriert, was die Gesamtlänge der Kurve ergibt. Dieser Prozess zeigt die enge Verbindung zwischen Differentiation und Integration, zwei fundamentalen Operationen der Analysis.
Das Verständnis der Bogenlänge fördert nicht nur das mathematische Denken, sondern ermöglicht auch die Lösung praktischer Probleme, bei denen präzise Längenmessungen von gekrümmten Pfaden erforderlich sind. Somit ist die Bogenlänge ein unverzichtbares Werkzeug in der modernen Wissenschaft und Technik.
Viel Spaß bei diesem Kurs! 🙂
Materialien
Arbeiten mit den Materialien
Um mit den Materialien arbeiten zu können, gehst du wie folgt vor:
- Klicke auf das Bild rechts neben dem Text
- Lade dir die PDF herunter und drucke das Blatt aus (Tipp: Am besten Doppelseitig)
- Sehe dir das unten verlinkte Lernvideo an.
- Fülle die Lücken auf dem Blatt parallel zum Video aus.
- Übe mit den Übungsaufgaben.
- Überprüfe ob du das Blatt richtig ausgefüllt. Klicke dafür auf das Bild im Fenster Kontrolle.
Lernvideo
Übungsaufgaben
Aufgabe Versuche dich an den folgenden interaktiven Aufgaben! (folgt noch)
Kontrolle
Nun ist es an der Zeit deine beschriebenen Materialien einmal selbst mit der Lösung zu vergleichen. Klicke auf das Bild um dir die Lösungen des Merkblattes anzuzeigen.
Korrigiere bei Bedarf!
