Stammfunktion und unbestimmtes Integral
Oder: Der Blick auf das Gesamte
Die Kapitel
Was erwartet dich
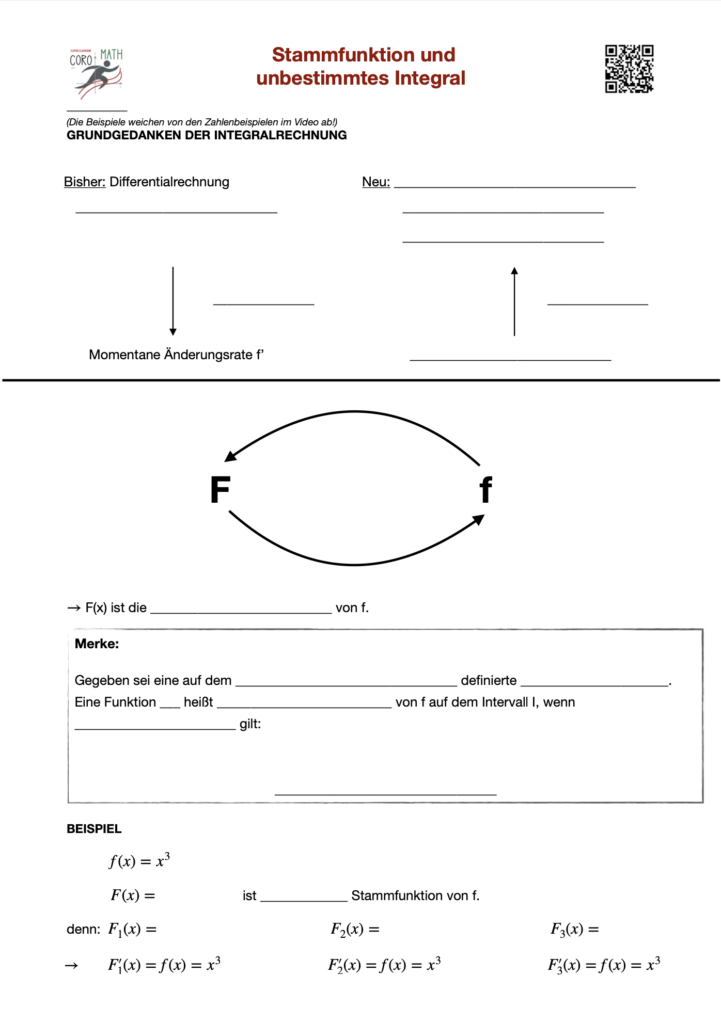
Eine Stammfunktion ist eine Funktion, deren Ableitung eine gegebene Funktion ergibt. Wenn wir also eine Funktion f(x)f(x)f(x) haben, suchen wir eine Funktion F(x)F(x)F(x), deren Ableitung f(x)f(x)f(x) ist. Das bedeutet, dass F'(x)=f(x) gilt. Stammfunktionen spielen eine zentrale Rolle in der Integralrechnung, da sie es uns ermöglichen, unbestimmte Integrale zu berechnen.
Das unbestimmte Integral ist eine allgemeine Form des Integrals und stellt die Menge aller möglichen Stammfunktionen einer Funktion dar. Wenn wir das unbestimmte Integral von f(x)f(x)f(x) bestimmen, erhalten wir eine Funktion F(x)F(x)F(x), die sich von der ursprünglichen Funktion durch eine Konstante unterscheidet. Diese Konstante nennt man das „Integrationskonstante“ und wird als +C+ C+C angegeben, weil jede Stammfunktion durch eine beliebige Konstante verschoben werden kann, ohne dass sich ihre Ableitung ändert.
Das unbestimmte Integral wird geschrieben als ∫f(x) dx\int f(x) \, dx∫f(x)dx, wobei das Symbol ∫\int∫ für „integrieren“ steht und dxdxdx anzeigt, dass wir bezüglich der Variable xxx integrieren. In der Praxis hilft uns das unbestimmte Integral dabei, die ursprüngliche Funktion aus ihrer Ableitung zurückzugewinnen und bildet die Grundlage für viele Anwendungen in der Physik, Technik und Wirtschaft.
Viel Spaß bei diesem Kurs! 🙂
Materialien
Arbeiten mit den Materialien
Um mit den Materialien arbeiten zu können, gehst du wie folgt vor:
- Klicke auf das Bild rechts neben dem Text
- Lade dir die PDF herunter und drucke das Blatt aus (Tipp: Am besten Doppelseitig)
- Sehe dir das unten verlinkte Lernvideo an.
- Fülle die Lücken auf dem Blatt parallel zum Video aus.
- Übe mit den Übungsaufgaben.
- Überprüfe ob du das Blatt richtig ausgefüllt. Klicke dafür auf das Bild im Fenster Kontrolle.
Lernvideo
Übungsaufgaben
Aufgabe Versuche dich an den folgenden interaktiven Aufgaben!
Berechne die Stammfunktion
Gib die Stammfunktion der folgenden Funktion an. Das Absolutglied wird als \( c \) angegeben:
Stammfunktion: