Wendepunkte und Krümmungsverhalten
Oder: Der Anstieg des Anstiegs
Die Kapitel
Was erwartet dich
Das Verständnis von Wendepunkten und dem Krümmungsverhalten einer Funktion ist ein zentraler Bestandteil der Kurvendiskussion in der Mathematik. Wendepunkte sind spezielle Punkte auf dem Graphen einer Funktion, an denen sich das Krümmungsverhalten ändert. Das bedeutet, dass die Funktion in einem Wendepunkt von einer Rechtskurve (konkav) zu einer Linkskurve (konvex) oder umgekehrt wechselt.
Um Wendepunkte zu finden, betrachtet man die zweite Ableitung der Funktion. Die zweite Ableitung beschreibt das Krümmungsverhalten des Graphen, also ob die Funktion nach oben oder nach unten „gekrümmt“ ist. Wenn die zweite Ableitung null wird und das Krümmungsverhalten in der Umgebung des Punktes wechselt, liegt ein Wendepunkt vor.
Das Krümmungsverhalten hilft uns, mehr über den Verlauf einer Funktion zu erfahren. Wenn die zweite Ableitung positiv ist, spricht man von einer Linkskurve (konvex), bei einer negativen zweiten Ableitung liegt eine Rechtskurve (konkav) vor. Wendepunkte geben uns daher wichtige Informationen über die Form und Struktur des Graphen einer Funktion.
In der Praxis spielen Wendepunkte und das Krümmungsverhalten eine Rolle in vielen Bereichen, wie etwa in der Physik zur Beschreibung von Bewegungen oder in der Wirtschaft, wenn es um die Analyse von Wachstums- und Kostenfunktionen geht.
Viel Spaß bei diesem Kurs! 🙂
Materialien
Arbeiten mit den Materialien
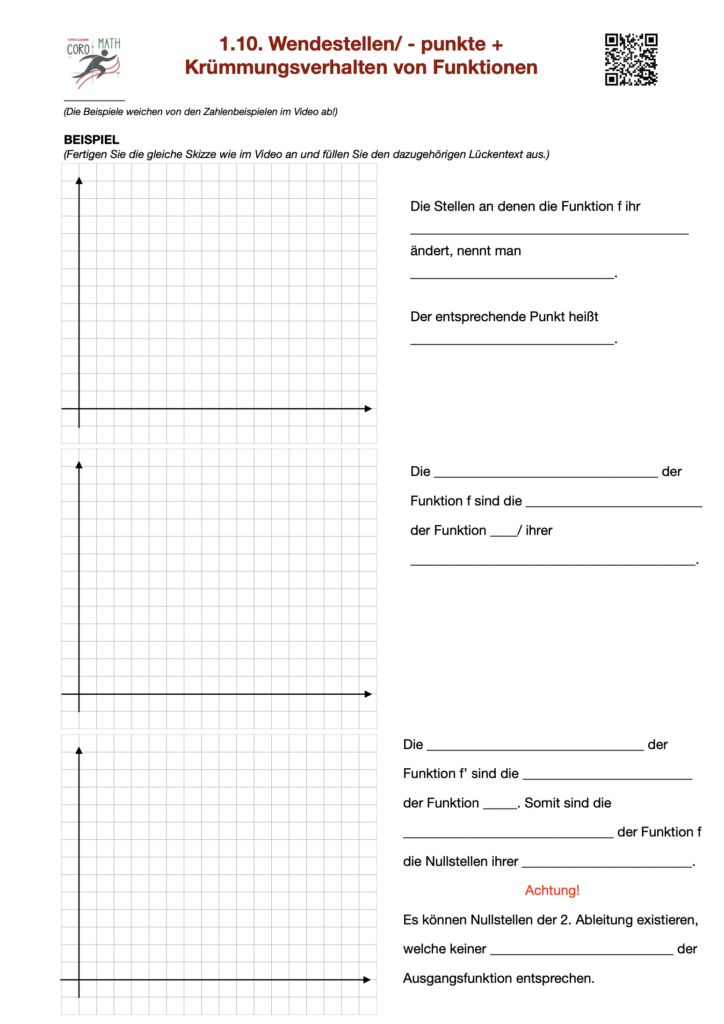
Um mit den Materialien arbeiten zu können, gehst du wie folgt vor:
- Klicke auf das Bild rechts neben dem Text
- Lade dir die PDF herunter und drucke das Blatt aus (Tipp: Am besten Doppelseitig)
- Sehe dir das unten verlinkte Lernvideo an.
- Fülle die Lücken auf dem Blatt parallel zum Video aus.
- Übe mit den Übungsaufgaben.
- Überprüfe ob du das Blatt richtig ausgefüllt. Klicke dafür auf das Bild im Fenster Kontrolle.
Lernvideo
Übungsaufgaben
Aufgabe Versuche dich an den folgenden interaktiven Aufgaben! Gib Dezimalzahlen auf die 2. Nachkommastelle gerundet ein. Sollte es keinen Wendepunkt geben, geben Sie „keine Wendepunkte“ ein.
Wendepunkte Berechnen
Wählen Sie eine Funktion aus und berechnen Sie die Wendepunkte. Geben Sie die Wendepunkte im Format (x|y); (x|y) ein.
Funktion: \( f(x) = \)
Lernst du gern mit Coromath?
Dann hilf uns und abonniere den YouTube-Kanal "Coromath"
Aktuell produziert die WebSite noch geringe Kosten. Mit der Implementierung weiterer Funktionen steigen diese. So wäre die Einbindung einer KI zum beantworten von Fragen möglich, jedoch auch sehr teuer. Daher freuen wir uns über jede Unterstützung, welche uns die Seite ausbauen lässt. Eine Einnahmemöglichkeit wäre die Monetarisierung des dazugehörigen YouTube-Kanals. Für ein Abo musst du nur auf das nebenstehende Bild klicken.