Stetigkeit von Funktionen
Oder: Ist der Übergang glatt?
Die Kapitel
Was erwartet dich
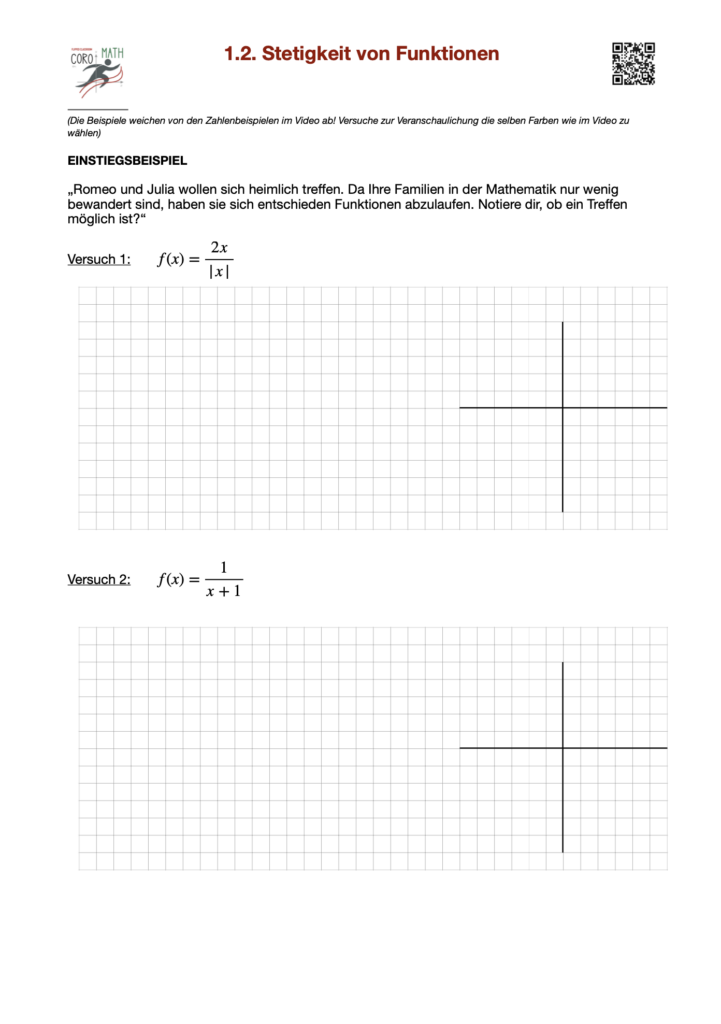
Die Stetigkeit einer Funktion ist ein grundlegendes Konzept in der Mathematik, das beschreibt, wie sich Funktionen verhalten, wenn ihre Eingabewerte leicht verändert werden. Eine Funktion ist stetig, wenn kleine Änderungen im Eingabewert nur kleine Änderungen im Ausgabewert verursachen. Das bedeutet, dass der Graph der Funktion keine Sprünge, Lücken oder Unterbrechungen aufweist.
Stell dir vor, du zeichnest den Graphen einer Funktion auf ein Blatt Papier. Wenn du den Stift auf das Papier setzt und den Graphen zeichnest, ohne den Stift abzusetzen, dann ist die Funktion stetig. Ein einfaches Beispiel ist die Linie y=2x+1y = 2x + 1y=2x+1. Egal, welche xxx-Werte du wählst, die Linie ist durchgehend und glatt.
Ein praktisches Beispiel für Stetigkeit ist eine gut ausgebaute Straße. Wenn du auf dieser Straße fährst, gibt es keine plötzlichen Löcher oder Sprünge, die dich überraschen könnten. Du kannst gleichmäßig und ohne Unterbrechung weiterfahren. Eine nicht-stetige Funktion wäre wie eine Straße mit vielen Schlaglöchern oder abrupten Abbrüchen, die deine Fahrt plötzlich stoppen könnten.
Mathematisch bedeutet Stetigkeit, dass der Funktionswert f(x)f(x)f(x) kontinuierlich ist und keine abrupten Veränderungen zeigt. Wenn du den Eingabewert xxx nur geringfügig änderst, ändert sich der Ausgabewert f(x)f(x)f(x) ebenfalls nur geringfügig. Dies ist eine wichtige Eigenschaft, die in vielen Bereichen der Mathematik und ihrer Anwendungen eine zentrale Rolle spielt.
Viel Spaß bei diesem Kurs! 🙂
Materialien
Arbeiten mit den Materialien
Um mit den Materialien arbeiten zu können, gehst du wie folgt vor:
- Klicke auf das Bild rechts neben dem Text
- Lade dir die PDF herunter und drucke das Blatt aus (Tipp: Am besten Doppelseitig)
- Sehe dir das unten verlinkte Lernvideo an.
- Fülle die Lücken auf dem Blatt parallel zum Video aus.
- Übe mit den Übungsaufgaben.
- Überprüfe ob du das Blatt richtig ausgefüllt. Klicke dafür auf das Bild im Fenster Kontrolle.
Lernvideo
Übungsaufgaben
Aufgabe: Versuche dich an den folgenden Interaktiven Aufgaben.
Lernst du gern mit Coromath?
Dann hilf uns und abonniere den YouTube-Kanal "Coromath"
Aktuell produziert die WebSite noch geringe Kosten. Mit der Implementierung weiterer Funktionen steigen diese. So wäre die Einbindung einer KI zum beantworten von Fragen möglich, jedoch auch sehr teuer. Daher freuen wir uns über jede Unterstützung, welche uns die Seite ausbauen lässt. Eine Einnahmemöglichkeit wäre die Monetarisierung des dazugehörigen YouTube-Kanals. Für ein Abo musst du nur auf das nebenstehende Bild klicken.